Torsion angle dynamics: Difference between revisions
CyanaAdmin (talk | contribs) |
|||
| (65 intermediate revisions by 6 users not shown) | |||
| Line 9: | Line 9: | ||
When compared with other structure calculation algorithms based on simulated annealing (Brünger, 1992), the principal difference of torsion angle dynamics is that it works with internal coordinates rather than Cartesian coordinates. Thereby the number of degrees of freedom is decreased about ten-fold, since the covalent structure parameters (bond lengths, bond angles, chiralities and planarities) are kept fixed at their optimal values during the calculation. The strong potentials required to preserve the covalent structure in conventional Cartesian space molecular dynamics and the concomitant high-frequency motions are absent in torsion angle dynamics. This results in a simpler potential energy function and the use of longer time-steps for the numerical integration of the equations of motion, and hence in higher efficiency of the structure calculation. An additional, practical advantage of working in torsion angle space is that this approach excludes inadvertent changes of chirality during the course of a structure calculation, which may happen with Cartesian space molecular dynamics (Schultze & Feigon, 1997). | When compared with other structure calculation algorithms based on simulated annealing (Brünger, 1992), the principal difference of torsion angle dynamics is that it works with internal coordinates rather than Cartesian coordinates. Thereby the number of degrees of freedom is decreased about ten-fold, since the covalent structure parameters (bond lengths, bond angles, chiralities and planarities) are kept fixed at their optimal values during the calculation. The strong potentials required to preserve the covalent structure in conventional Cartesian space molecular dynamics and the concomitant high-frequency motions are absent in torsion angle dynamics. This results in a simpler potential energy function and the use of longer time-steps for the numerical integration of the equations of motion, and hence in higher efficiency of the structure calculation. An additional, practical advantage of working in torsion angle space is that this approach excludes inadvertent changes of chirality during the course of a structure calculation, which may happen with Cartesian space molecular dynamics (Schultze & Feigon, 1997). | ||
To fully exploit the potential advantages of torsion angle dynamics for macromolecular structure calculation, its implementation has to take account of the fact that the Lagrange equations of motion with torsion angles as degrees of freedom are more complex than Newton’s equations in Cartesian coordinates. The computation time for “naïve” (but by no means simple) approaches (Mazur & Abagyan, 1989; Mazur et al., 1991) to torsion angle dynamics rises with the third power of the system size, which renders these algorithms unsuitable for use with macromolecules. CYANA gets around this potential drawback by using a fast recursive implementation of the equations of motion that was originally developed for spacecraft dynamics and robotics (Jain et al., 1993), which entails a computational effort proportional to | To fully exploit the potential advantages of torsion angle dynamics for macromolecular structure calculation, its implementation has to take account of the fact that the Lagrange equations of motion with torsion angles as degrees of freedom are more complex than Newton’s equations in Cartesian coordinates. The computation time for “naïve” (but by no means simple) approaches (Mazur & Abagyan, 1989; Mazur et al., 1991) to torsion angle dynamics rises with the third power of the system size, which renders these algorithms unsuitable for use with macromolecules. CYANA gets around this potential drawback by using a fast recursive implementation of the equations of motion that was originally developed for spacecraft dynamics and robotics (Jain et al., 1993), which entails a computational effort proportional to the number of torsion angles. With the fast torsion angle dynamics algorithm in CYANA the advantages of torsion angle dynamics, especially that much longer integration time steps can be used, are effective for molecules of all sizes. | ||
=== NMR structure calculation versus molecular dynamics simulation === | === NMR structure calculation versus molecular dynamics simulation === | ||
There is a fundamental difference between molecular dynamics simulation that has the aim of simulating the trajectory of a molecular system as realistically as possible in order to extract molecular quantities of interest and NMR structure calculation that is driven by experimental restraints | There is a fundamental difference between molecular dynamics simulation that has the aim of simulating the trajectory of a molecular system as realistically as possible in order to extract molecular quantities of interest and NMR structure calculation that is driven by experimental restraints. | ||
Classical molecular dynamics simulations rely on a full empirical force field to ensure proper stereochemistry, and are generally run at a constant temperature, close to room temperature. Substantial amounts of computation time are required because the empirical energy function includes long-range pair interactions that are time-consuming to evaluate, and because conformation space is explored slowly at room temperature. | |||
When molecular dynamics algorithms are used for NMR structure calculations, however, the objective is quite different. Here, such algorithms simply provide a means to efficiently optimize a target function that takes the role of the potential energy. Details of the calculation, such as the course of a trajectory, are unimportant, as long as its end point comes close to the global minimum of the target function. | |||
Therefore, the efficiency of NMR structure calculation can be enhanced by simplification or modification of the force field and/or the algorithm that do not significantly alter the location of the global minimum (the correctly folded structure) but shorten, in terms of the computation time needed, the path by which it can be reached from the start conformation. | |||
A typical “geometric” force field used in NMR structure calculation therefore retains only the most important part of the non-bonded interaction by a simple repulsive potential that replaces the Lennard-Jones and electrostatic interactions of the full empirical energy function. This short-range repulsive function can be calculated much faster and significantly facilitates large-scale conformational changes that are required during the folding process by lowering energy barriers induced by the overlap of atoms. | |||
== Tree structure == | |||
The key idea of the fast torsion angle dynamics algorithm in CYANA is to exploit the fact that a chain molecule such as a protein or nucleic acid can be represented in a natural way as a tree structure consisting of | |||
The key idea of the fast torsion angle dynamics algorithm in CYANA is to exploit the fact that a chain molecule such as a protein or nucleic acid can be represented in a natural way as a tree structure consisting of ''n'' + 1 rigid bodies or “clusters” that are connected by ''n'' rotatable bonds. Each rigid body is made up of one or several mass points (atoms) with fixed relative positions. The tree structure starts from a base, typically at the N-terminus of the polypeptide chain, and terminates with “leaves” at the ends of the side-chains and at the C-terminus. The only degrees of freedom are rotations about single bonds, and parameters that define the position and orientation of the molecule in space. The clusters are numbered from 0 to ''n''. The base cluster has the number ''k'' = 0. Each of the other clusters, with numbers ''k'' ≥ 1, has a single nearest neighbor in the direction toward the base, which has a number ''p''(''k'') < ''k''. The torsion angle between the rigid bodies ''p''(''k'') and ''k'' is denoted by ''θ<sub>k</sub>''. The conformation of the molecule is uniquely specified by the values of all torsion angles, (''θ<sub>1</sub>'',…,''θ<sub>n</sub>''). | |||
Fig. 1. (a) Tree structure of torsion angles for the tripeptide Val-Ser-Ile. Circles represent rigid units. Rotatable bonds are indicated by arrows that point towards the part of the structure that is rotated if the corresponding torsion angle is changed. (b) Excerpt from the tree structure formed by the torsion angles of a molecule, and definition of quantities required by the CYANA torsion angle dynamics algorithm. | |||
[[Image:TreeStructureRigidBodies.jpg|thumb|500px|Fig. 1. (a) Tree structure of torsion angles for the tripeptide Val-Ser-Ile. Circles represent rigid units. Rotatable bonds are indicated by arrows that point towards the part of the structure that is rotated if the corresponding torsion angle is changed. (b) Excerpt from the tree structure formed by the torsion angles of a molecule, and definition of quantities required by the CYANA torsion angle dynamics algorithm.]] | |||
The following quantities are defined for each cluster ''k'' (see Fig. 1): the “reference point”, ''r<sub>k</sub>'', which is the position vector of the end point of the bond between the clusters ''p''(''k'') and ''k''; <math>v_k = \dot{r}_k</math>, the velocity of the reference point; ''ω<sub>k</sub>'', the angular velocity vector of the cluster; ''Y<sub>k</sub>'', the vector from the reference point to the center of mass of the cluster; ''m<sub>k</sub>'', the mass of the cluster ''k''; ''I<sub>k</sub>'', the inertia tensor of the cluster ''k'' with respect to the reference point, given by | |||
:<math>\textstyle I_k = \sum_\alpha m_\alpha I(y_\alpha)</math> | |||
where the sum runs over all atoms in the cluster ''k'', ''m<sub>α</sub>'' is the mass of the atom ''α'', ''y<sub>α</sub>'' is the vector from the reference point of cluster ''k'' to the atom ''α'', and ''I''(''y<sub>α</sub>'') is the symmetric 3 × 3 matrix defined by the relation ''I''(''y'') = ''y'' Λ (''x'' Λ ''y'') for all three-dimensional vectors ''x''. The symbol “Λ” denotes the vector product. All position vectors are in an inertial frame of reference that is fixed in space. | |||
== Kinetic energy == | |||
The angular velocity vector ''ω<sub>k</sub>'' and the linear velocity ''v<sub>k</sub>'' of the reference point of the rigid body ''k'' are calculated recursively from the corresponding quantities of the preceding rigid body ''p''(''k''): | |||
:<math>\omega_k = \omega_{p(k)} + e_k \dot{\theta}_k</math>, | |||
:<math>v_k = v_{p(k)} - (r_k - r_{p(k)}) \wedge \omega_{p(k)}</math>. | |||
The kinetic energy can then be computed in a linear loop over all rigid bodies: | The kinetic energy can then be computed in a linear loop over all rigid bodies: | ||
:<math>E_{\text{kin}}=\frac{1}{2}\sum_{k=0}^n[m_k v_k^2 + \omega_k \cdot I_k \omega_k + 2v_k\cdot(\omega_k \wedge m_k Y_k)]</math>. | |||
== Potential energy = target function == | |||
For torsion angle dynamics the CYANA [[target function]] (Güntert et al., 1991; Güntert et al., 1997), ''V'', has the role of the potential energy, ''E''<sub>pot</sub> = ''V'', and energies are reported in units of the target function ''V'', i.e. Å<sup>2</sup>, in the current version of CYANA. If energies and temperatures are to be reported in their standard units of kJ/mol and K, we assume that ''E''<sub>pot</sub> = ''w''<sub>0</sub>''V'', with an overall (arbitrary) scaling factor ''w''<sub>0</sub> = 10 kJ mol<sup>-1</sup>Å<sup>-2</sup>. | |||
Because the target function is not a physical potential, there is no unique “natural” way to define the energy and temperature scale for protein structure calculations. | |||
== Generalized forces = torques = –gradient of the target function == | |||
The torques about the rotatable bonds, i.e., the negative gradients of the potential energy or target function with respect to torsion angles, -∇''V''(''θ''), are calculated by a fast recursive algorithm (Abe et al., 1984). The gradient of the target function can be calculated efficiently because the target function is a sum of functions of individual interatomic distances and torsion angles. The partial derivative of the target function ''V'' with respect to a torsion angle ''θ<sub>k</sub>'' is given by | |||
:<math>\frac{\partial V}{\partial\theta_k} = -e_k\cdot f_k - (e_k \wedge r_k)\cdot g_k + 2 w_a \sum_{i\in I_a} w_i\left[1-\left(\frac{\Delta_i}{\Gamma_i}\right)^2\right]\Delta_i \delta_{ik}</math> | |||
with | with | ||
=== Equations of motion | :<math>f_k = \sum_{c=u,l,v} w_c \sum_{(\alpha,\beta)\in I_c\atop\alpha\in M_k} w_{\alpha\beta}^c 2\,\frac{d_{\alpha\beta}-b_{\alpha\beta}}{d_{\alpha\beta}}(r_\alpha\wedge r_\beta)</math>, | ||
:<math>g_k = \sum_{c=u,l,v} w_c \sum_{(\alpha,\beta)\in I_c\atop\alpha\in M_k} w_{\alpha\beta}^c 2\,\frac{d_{\alpha\beta}-b_{\alpha\beta}}{d_{\alpha\beta}}(r_\alpha - r_\beta)</math>. | |||
''r<sub>α</sub>'' and ''r<sub>β</sub>'' are the position vectors of the atoms ''α'' and ''β'', and ''M<sub>k</sub>'' denotes the set of all atoms whose position is affected by a change of the torsion angle ''θ<sub>k</sub>'' if the base cluster is held fixed. Because ''M<sub>k</sub>'' is a subset of ''M''<sub>''p''(''k'')</sub>, the quantities ''f<sub>k</sub>'' and ''g<sub>k</sub>'' can be calculated recursively for ''k'' = ''n'',''n'' - 1,…,1 starting from the leaves of the tree structure by evaluating the interaction for each atom pair (''α'',''β'') only once. | |||
== Equations of motion == | |||
The calculation of the torsional accelerations, i.e. the second time derivatives of the torsion angles, is the crucial point of a torsion angle dynamics algorithm. The equations of motion for a classical mechanical system with generalized coordinates are the Lagrange equations | The calculation of the torsional accelerations, i.e. the second time derivatives of the torsion angles, is the crucial point of a torsion angle dynamics algorithm. The equations of motion for a classical mechanical system with generalized coordinates are the Lagrange equations | ||
:<math>\frac{d}{dt}\left(\frac{\partial L}{\partial\dot\theta_k}\right) - \frac{\partial L}{\partial\theta_k} = 0</math> | |||
with the Lagrange function | with the Lagrange function ''L'' = ''E''<sub>kin</sub> - ''E''<sub>pot</sub>. They lead to equations of motion of the form | ||
:<math>M(\theta)\ddot\theta + C(\theta,\dot\theta) = 0</math>. | |||
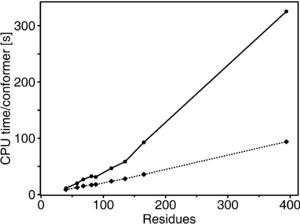
Fig. 2. Dependence on the protein size of the CPU time for the calculation of one conformer using the CYANA torsion angle dynamics algorithm with 4000 time steps on two different computers (solid and dotted lines) (Güntert et al., 1997). | [[Image:CPUtimeVsSize.jpg|thumb|300px|Fig. 2. Dependence on the protein size of the CPU time for the calculation of one conformer using the CYANA torsion angle dynamics algorithm with 4000 time steps on two different computers (solid and dotted lines) (Güntert et al., 1997).]] | ||
In the case of n torsion angles as degrees of freedom, the n × n mass matrix ''M''(''θ'') and the ''n''-dimensional vector <math>C(\theta,\dot\theta)</math>, can be calculated explicitly (Mazur & Abagyan, 1989; Mazur et al., 1991). To generate a trajectory this linear set of n equations would have to be solved in each time step for the torsional accelerations <math>\ddot\theta</math>, formally by | |||
:<math>\ddot\theta = M(\theta)^{-1}C(\theta,\dot\theta)</math>. | |||
This requires a computational effort proportional to ''n''<sup>3</sup>, which is prohibitively expensive for larger systems. Therefore, in CYANA the fast recursive algorithm of (Jain et al., 1993) is implemented to compute the torsional accelerations, which makes explicit use of the tree structure of the molecule in order to obtain with a computational effort that is only proportional to ''n''. The mathematical details and a proof of correctness of the CYANA torsion angle dynamics algorithm are given in (Jain et al., 1993). | |||
== Torsional accelerations == | |||
The algorithm of (Jain et al., 1993) computes a factorization of the inverse of the mass matrix, ''M''(''θ'')<sup>-1</sup>, into a product of highly sparse matrices with non-zero elements only in 6 × 6 blocks on or near the diagonal. As a result, the torsional accelerations can be obtained by executing a series of three linear loops over all rigid bodies similar to the single loop that is needed to compute the kinetic energy, ''E''<sub>kin</sub>. | |||
The computation of the torsional accelerations by the algorithm of Jain et al. (1993) is initialized by calculating for all rigid bodies, ''k'' = 1,…,n, the six-dimensional vectors ''a<sub>k</sub>'', ''e<sub>k</sub>'' and ''z<sub>k</sub>'': | |||
:<math>a_k = \begin{bmatrix}\omega_k \wedge e_k)\dot\theta_k \\\omega_{p(k)} \wedge (v_k - v_{p(k)})\end{bmatrix}</math>, | |||
:<math>e_k = \begin{bmatrix}e_k\\0\end{bmatrix}</math>, | |||
:<math>a_k = \begin{bmatrix}\omega_k \wedge I_k\omega_k\\(\omega_k \cdot m_k Y_k)\omega_k - |\omega_k|^2 m_k Y_k\end{bmatrix}</math>, | |||
and the 6 × 6 matrices ''P<sub>k</sub>'' and ''φ<sub>k</sub>'': | |||
:<math>P_k = \begin{bmatrix}I_k & m_k A(Y_k)\\-m_k A(Y_k) & m_k 1_3\end{bmatrix}</math>, | |||
:<math>\phi_k = \begin{bmatrix}1_3 & A(r_k-r_{p(k)})\\0_3 & 1_3\end{bmatrix}</math>. | |||
0<sub>3</sub> is the 3 × 3 zero matrix, 1<sub>3</sub> is the 3 × 3 unit matrix, and ''A''(''y'') denotes the antisymmetric 3 × 3 matrix associated with the cross product, i.e., ''A''(''y'')''x'' = ''y'' Λ ''x'' for all vectors ''x''. | |||
Next, several auxiliary quantities are calculated by executing a recursive loop over all rigid bodies in the backward direction, ''k'' = ''n'',''n'' - 1,…,1: | |||
:<math>\begin{align}D_k &= e_k \cdot P_k e_k\\ | |||
G_k &= P_k e_k/D_k\\ | |||
\epsilon_k &= -e_k \cdot (z_k + P_k a_k) - \frac{\partial V}{\partial\theta_k}\\ | |||
P_{p(k)} &\leftarrow P_{p(k)} + \phi_k(P_k - G_k e_k^T P_k)\phi_k^T\\ | |||
z_{p(k)} &\leftarrow z_{p(k)} + \phi_k(z_k + P_k a_k - G_k \epsilon_k) | |||
\end{align}</math> | |||
''D<sub>k</sub>'' and ''ε<sub>k</sub>'' are scalars, ''G<sub>k</sub>'' is a six-dimensional vector, and “←” means: “assign the result of the expression on the right hand side to the variable on the left hand side.” Finally, the tor-sional accelerations are obtained by executing another recursive loop over all rigid bodies in the forward direction, ''k'' = 1,…,''n'': | |||
:<math>\begin{align}\alpha_k &= \phi_k^T \alpha_{p(k)}\\ | |||
\ddot\theta_k &= \epsilon_k/D_k - G_k\cdot\alpha_k\\ | |||
\alpha_k &\leftarrow \alpha_k + e_k \ddot\theta_k + a_k | |||
\end{align}</math> | |||
=== | The auxiliary quantities ''α<sub>k</sub>'' are six-dimensional vectors, with ''α''<sub>0</sub> being equal to the zero vector. | ||
== Time step == | |||
=== Leap-frog algorithm === | |||
The integration scheme for the equations of motion in torsion angle dynamics (Mathiowetz et al., 1994) is a variant of the “leap-frog” algorithm used in Cartesian space molecular dynamics (Allen & Tildesley, 1987). To obtain a trajectory, the equations of motion are numerically integrated by advancing the ''i'' = 1,…,''n'' (generalized) coordinates ''q<sub>i</sub>'' and velocities <math>\dot q_i</math> that describe the system by a small but finite time step Δ''t'': | |||
:<math>\begin{align} | |||
\dot q_i(t + \Delta t/2) &= \dot q_i(t - \Delta t/2) + \Delta t \ddot q_i(t) + O(\Delta t^3)\\ | |||
q_i(t + \Delta t) &= q_i(t) + \dot q_i(t + \Delta t/2) + O(\Delta t^3) | |||
\end{align}</math> | |||
The degrees of freedom, ''q<sub>i</sub>'', are the Cartesian coordinates of the atoms in conventional molecular dynamics simulation, or the torsion angles in CYANA. The ''O''(Δ''t''<sup>3</sup>) terms indicate that the errors with respect to the exact solution incurred by the use of a finite time step Δ''t'' are proportional to Δ''t''<sup>3</sup>. | |||
=== Temperature control === | |||
The time step Δ''t'' must be small enough to sample adequately the fastest motions. Because the fastest motions in conventional molecular dynamics simulation are oscillations of bond lengths and bond angles, which are “frozen” in torsion angle space, longer time steps can be used for torsion angle dynamics than for molecular dynamics in Cartesian space. | |||
In practical applications with proteins time steps of about 100, 30 and 7 fs at low (1 K), medium (400 K) and high (10000 K) temperatures, respectively, can be used in torsion angle dynamics calculations with CYANA (Güntert et al., 1997), whereas time steps in Cartesian space molecular dynamics simulation generally have to be in the range of 2 ns. The concomitant fast exploration of conformation space provides the basis for the efficient CYANA structure calculation protocol. | In practical applications with proteins time steps of about 100, 30 and 7 fs at low (1 K), medium (400 K) and high (10000 K) temperatures, respectively, can be used in torsion angle dynamics calculations with CYANA (Güntert et al., 1997), whereas time steps in Cartesian space molecular dynamics simulation generally have to be in the range of 2 ns. The concomitant fast exploration of conformation space provides the basis for the efficient CYANA structure calculation protocol. | ||
The temperature is controlled by weak coupling to an external bath (Berendsen et al., 1984). Using a similar approach, the length of the time step is adapted automatically based on the accuracy of energy conservation (Güntert et al., 1997). | The temperature is controlled by weak coupling to an external bath (Berendsen et al., 1984). Using a similar approach, the length of the time step is adapted automatically based on the accuracy of energy conservation (Güntert et al., 1997). | ||
A time step, | |||
(1) On the basis of the torsional positions, | === Time step === | ||
(2) Using the Cartesian coordinates, calculate the potential energy function | |||
(3) Determine the time-step, | A time step, ''t'' → ''t'' + Δ''t'', that follows a preceding time step, ''t'' - Δ''t''' → ''t'', consists of the following parts: | ||
(1) On the basis of the torsional positions, ''θ''(''t''), [[calculate the Cartesian coordinates|Coordinate generation]] of all atoms (Güntert, 1993). | |||
(2) Using the Cartesian coordinates, calculate the [[target function]], i.e. the potential energy function ''E''<sub>pot</sub>(''t'') = ''E''<sub>pot</sub>(''θ''(''t'')), and its gradient ∇''E''<sub>pot</sub>(''t''). | |||
(4) Adapt the temperature by scaling of the torsional velocities, i.e., replace | |||
(3) Determine the time-step, Δ''t'' = ''λ<sub>ε</sub>''Δ''t''', using the time-step scaling factor | |||
:<math>\lambda_\epsilon = \min\left(\lambda_\epsilon^\max,\sqrt{1+\frac{\epsilon^\text{ref} - \epsilon(t)}{\tau\epsilon(t)}}\right)</math>. | |||
''λ<sub>ε</sub>'' is based on the reference value for the relative accuracy of energy conservation, ''ε''<sup>ref</sup>, and on the relative change of the total energy, ''E'' = ''E''<sub>kin</sub> + ''E''<sub>pot</sub>, in the preceding time-step, ''ε''(''t''), as given by | |||
:<math>\epsilon(t) = \left|\frac{E(t)-E(t-\Delta t')}{E(t)}\right|</math>. | |||
<math>\lambda_\epsilon^\max</math> is the maximally allowed value of the scaling factor, which is set to 1.025 in CYANA. The time constant, ''τ'' >> 1, is a user-defined parameter that is measured in units of the time-step. Typically, a value of ''τ'' = 20 is used for structure calculations with CYANA. To calculate ''ε''(''t''), the total energy ''E''(''t'') is evaluated before velocity scaling is applied (step 4 below), whereas for ''E''(''t'' - Δ''t''') the value after velocity scaling in the preceding time-step is used. Thus, the measurement of the accuracy of energy conservation is not affected by the scaling of velocities. An exact algorithm would yield ''E''(''t'') = ''E''(''t'' - Δ''t''') and consequently ''ε''(''t'') = 0. | |||
(4) Adapt the temperature by scaling of the torsional velocities, i.e., replace <math>\dot\theta_i(t - \Delta t'/2)</math> by <math>\lambda_T\dot\theta_i(t - \Delta t'/2)</math> and <math>\dot\theta_e(t)</math> by <math>\lambda_T\dot\theta_e(t)</math> (see step 7 below for the definition of <math>\dot\theta_e(t)</math>). The velocity scaling factor, ''λ<sub>T</sub>'', is given by (Berendsen et al., 1984) | |||
:<math>\lambda_T = \sqrt{1+\frac{T^\text{ref}-T(t)}{\tau T(t)}}</math>, | |||
( | where ''T''<sup>ref</sup> is the reference value of the temperature. The instantaneous temperature, ''T''(''t''), is given by ''T''(''t'') = 2 ''E''<sub>kin</sub>(''t'')/''nk''<sub>B</sub>, where ''E''<sub>kin</sub>(''t'') is the kinetic energy at time ''t'', ''n'' denotes the number of torsion angles and ''k''<sub>B</sub> is the Boltzmann constant. Temperature control by coupling to an external heat bath (and time-step control) can be turned off by setting ''τ'' = ∞. | ||
( | (5) Calculate the torsional accelerations, <math>\ddot\theta(t)=\ddot\theta(\theta(t),\dot\theta_e(t))</math>, using equations [3–6]. | ||
(6) Calculate the new velocities at half time-step, | |||
:<math>\dot\theta(t + \Delta t/2) = \dot\theta(t - \Delta t'/2) + \frac{\Delta t+\Delta t'}{2} \ddot\theta(t)</math>. | |||
(7) Calculate the new estimated velocities at full time step, | |||
:<math>\dot\theta_e(t + \Delta t) = \left(1+\frac{\Delta t}{\Delta t+\Delta t'}\right)\dot\theta(t + \Delta t/2) - \frac{\Delta t}{\Delta t+\Delta t'}{2} \dot\theta(t-\Delta t'/2)</math>. | |||
(8) Calculate the new torsional positions, | |||
:<math>\theta(t + \Delta t) = \theta(t) + \Delta t \dot\theta(t+\Delta t/2)</math>. | |||
The algorithm is initialized by setting ''t'' = 0, Δ''t''' = Δ''t'' and <math>\dot\theta_e(0)=\dot\theta(-\Delta t/2)</math>. The initial torsional velocities, <math>\dot\theta(-\Delta t/2)</math>, are chosen randomly from a normal distribution with zero mean value and a standard deviation which ensures that the initial temperature has a predefined value, ''T''(0). Once the time step ''t'' → ''t'' + Δ''t'' is completed by going through the operations 1 to 8, ''t'' is replaced by ''t'' + Δ''t'', and Δ''t''' by Δ''t''. | |||
=== | === Accuracy of acceleration calculation === | ||
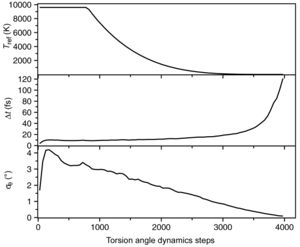
[[Image:Schedule.jpg|thumb|300px|Fig. 3. Plots versus the number of torsion angle dynamics steps for a structure calculation with simulated annealing for the protein cyclophilin A. (a) Temperature of the heat bath to which the system is weakly coupled. (b) Integration time step length, Δ''t''. (c) RMS torsion angle change, ''σ<sub>θ</sub>'', between successive time steps. Data are averaged over 50 time steps and 80 independently calculated conformers (Güntert et al., 1997).]] | |||
Unlike the situation in Cartesian dynamics, where the accelerations are a function of the positions only, the torsional accelerations also depend on the velocities. These, however, are only known at half time-steps, whereas the positions and accelerations are required at full time-steps. In step 7 the presently used algorithm employs linear extrapolation to obtain an estimate of the velocity after the full time-step, <math>\dot\delta_e(t)</math>, which is used in the next integration step to calculate the torsional accelerations (step 5). They are therefore beset with an additional error that could be eliminated by iterating the steps 5–7. In general, no significant improvement can be observed after one iteration (Mathiowetz et al., 1994). Using <math>\dot\theta_e(t)</math> instead of <math>\dot\theta(t)</math> introduces an additional error of order ''O''(Δ''t''<sup>3</sup>) into the velocity calculation of the leap-frog algorithm in step 6. However, the intrinsic accuracy of the velocity step is also ''O''(Δ''t''<sup>3</sup>). Thus, using the estimated velocities, <math>\dot\delta_e(t)</math>, does not change the order of accuracy of the integration algorithm. Each iteration of steps 5–7 requires the calculation of the torsional accelerations which, in general, takes as long as the calculation of the target function and its gradient. It is therefore more efficient to slightly decrease the time step, Δ''t'', than to perform steps 5–7 twice in each integration step. The situation could be different if a full physical force field were used, since then the calculation of torsional accelerations would require only a negligible fraction of the total computation time. | |||
( | |||
Since in structure calculations with torsion angle dynamics the time-steps are made as long as possible a safeguard against occasional strong violations of energy conservation was introduced: If the total energy, ''E'', has changed by more than 10% in a single time-step, this time-step is rejected and replaced by two time-steps of half length. | |||
step | |||
== References == | == References == | ||
Latest revision as of 19:30, 25 February 2023
Introduction
Torsion angle dynamics versus other structure calculation algorithms
The structure calculation algorithm in CYANA is based on the idea of simulated annealing (Kirkpatrick et al., 1983) by molecular dynamics simulation in torsion angle space. The distinctive feature of molecular dynamics simulation when compared to the straightforward minimization of a target function is the presence of kinetic energy that allows overcoming barriers of the potential surface, which reduces greatly the problem of becoming trapped in local minima.
Torsion angle dynamics, i.e. molecular dynamics simulation using torsion angles instead of Cartesian coordinates as degrees of freedom, provides at present the most efficient way to calculate NMR structures of biological macromolecules. The only degrees of freedom are the torsion angles, i.e. rotations about single bonds, such that the conformation of the molecule is uniquely specified by the values of all torsion angles. Covalent bonds that are incompatible with a tree structure because they would introduce closed flexible rings, for example disulphide bridges, are treated, as in Cartesian space dynamics, by distance constraints.
When compared with other structure calculation algorithms based on simulated annealing (Brünger, 1992), the principal difference of torsion angle dynamics is that it works with internal coordinates rather than Cartesian coordinates. Thereby the number of degrees of freedom is decreased about ten-fold, since the covalent structure parameters (bond lengths, bond angles, chiralities and planarities) are kept fixed at their optimal values during the calculation. The strong potentials required to preserve the covalent structure in conventional Cartesian space molecular dynamics and the concomitant high-frequency motions are absent in torsion angle dynamics. This results in a simpler potential energy function and the use of longer time-steps for the numerical integration of the equations of motion, and hence in higher efficiency of the structure calculation. An additional, practical advantage of working in torsion angle space is that this approach excludes inadvertent changes of chirality during the course of a structure calculation, which may happen with Cartesian space molecular dynamics (Schultze & Feigon, 1997).
To fully exploit the potential advantages of torsion angle dynamics for macromolecular structure calculation, its implementation has to take account of the fact that the Lagrange equations of motion with torsion angles as degrees of freedom are more complex than Newton’s equations in Cartesian coordinates. The computation time for “naïve” (but by no means simple) approaches (Mazur & Abagyan, 1989; Mazur et al., 1991) to torsion angle dynamics rises with the third power of the system size, which renders these algorithms unsuitable for use with macromolecules. CYANA gets around this potential drawback by using a fast recursive implementation of the equations of motion that was originally developed for spacecraft dynamics and robotics (Jain et al., 1993), which entails a computational effort proportional to the number of torsion angles. With the fast torsion angle dynamics algorithm in CYANA the advantages of torsion angle dynamics, especially that much longer integration time steps can be used, are effective for molecules of all sizes.
NMR structure calculation versus molecular dynamics simulation
There is a fundamental difference between molecular dynamics simulation that has the aim of simulating the trajectory of a molecular system as realistically as possible in order to extract molecular quantities of interest and NMR structure calculation that is driven by experimental restraints.
Classical molecular dynamics simulations rely on a full empirical force field to ensure proper stereochemistry, and are generally run at a constant temperature, close to room temperature. Substantial amounts of computation time are required because the empirical energy function includes long-range pair interactions that are time-consuming to evaluate, and because conformation space is explored slowly at room temperature.
When molecular dynamics algorithms are used for NMR structure calculations, however, the objective is quite different. Here, such algorithms simply provide a means to efficiently optimize a target function that takes the role of the potential energy. Details of the calculation, such as the course of a trajectory, are unimportant, as long as its end point comes close to the global minimum of the target function.
Therefore, the efficiency of NMR structure calculation can be enhanced by simplification or modification of the force field and/or the algorithm that do not significantly alter the location of the global minimum (the correctly folded structure) but shorten, in terms of the computation time needed, the path by which it can be reached from the start conformation.
A typical “geometric” force field used in NMR structure calculation therefore retains only the most important part of the non-bonded interaction by a simple repulsive potential that replaces the Lennard-Jones and electrostatic interactions of the full empirical energy function. This short-range repulsive function can be calculated much faster and significantly facilitates large-scale conformational changes that are required during the folding process by lowering energy barriers induced by the overlap of atoms.
Tree structure
The key idea of the fast torsion angle dynamics algorithm in CYANA is to exploit the fact that a chain molecule such as a protein or nucleic acid can be represented in a natural way as a tree structure consisting of n + 1 rigid bodies or “clusters” that are connected by n rotatable bonds. Each rigid body is made up of one or several mass points (atoms) with fixed relative positions. The tree structure starts from a base, typically at the N-terminus of the polypeptide chain, and terminates with “leaves” at the ends of the side-chains and at the C-terminus. The only degrees of freedom are rotations about single bonds, and parameters that define the position and orientation of the molecule in space. The clusters are numbered from 0 to n. The base cluster has the number k = 0. Each of the other clusters, with numbers k ≥ 1, has a single nearest neighbor in the direction toward the base, which has a number p(k) < k. The torsion angle between the rigid bodies p(k) and k is denoted by θk. The conformation of the molecule is uniquely specified by the values of all torsion angles, (θ1,…,θn).
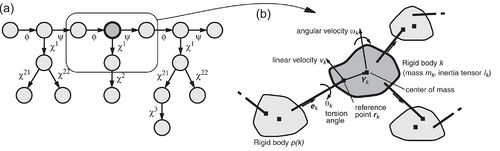
The following quantities are defined for each cluster k (see Fig. 1): the “reference point”, rk, which is the position vector of the end point of the bond between the clusters p(k) and k; , the velocity of the reference point; ωk, the angular velocity vector of the cluster; Yk, the vector from the reference point to the center of mass of the cluster; mk, the mass of the cluster k; Ik, the inertia tensor of the cluster k with respect to the reference point, given by
where the sum runs over all atoms in the cluster k, mα is the mass of the atom α, yα is the vector from the reference point of cluster k to the atom α, and I(yα) is the symmetric 3 × 3 matrix defined by the relation I(y) = y Λ (x Λ y) for all three-dimensional vectors x. The symbol “Λ” denotes the vector product. All position vectors are in an inertial frame of reference that is fixed in space.
Kinetic energy
The angular velocity vector ωk and the linear velocity vk of the reference point of the rigid body k are calculated recursively from the corresponding quantities of the preceding rigid body p(k):
- ,
- .
The kinetic energy can then be computed in a linear loop over all rigid bodies:
- .
Potential energy = target function
For torsion angle dynamics the CYANA target function (Güntert et al., 1991; Güntert et al., 1997), V, has the role of the potential energy, Epot = V, and energies are reported in units of the target function V, i.e. Å2, in the current version of CYANA. If energies and temperatures are to be reported in their standard units of kJ/mol and K, we assume that Epot = w0V, with an overall (arbitrary) scaling factor w0 = 10 kJ mol-1Å-2.
Because the target function is not a physical potential, there is no unique “natural” way to define the energy and temperature scale for protein structure calculations.
Generalized forces = torques = –gradient of the target function
The torques about the rotatable bonds, i.e., the negative gradients of the potential energy or target function with respect to torsion angles, -∇V(θ), are calculated by a fast recursive algorithm (Abe et al., 1984). The gradient of the target function can be calculated efficiently because the target function is a sum of functions of individual interatomic distances and torsion angles. The partial derivative of the target function V with respect to a torsion angle θk is given by
with
- ,
- .
rα and rβ are the position vectors of the atoms α and β, and Mk denotes the set of all atoms whose position is affected by a change of the torsion angle θk if the base cluster is held fixed. Because Mk is a subset of Mp(k), the quantities fk and gk can be calculated recursively for k = n,n - 1,…,1 starting from the leaves of the tree structure by evaluating the interaction for each atom pair (α,β) only once.
Equations of motion
The calculation of the torsional accelerations, i.e. the second time derivatives of the torsion angles, is the crucial point of a torsion angle dynamics algorithm. The equations of motion for a classical mechanical system with generalized coordinates are the Lagrange equations
with the Lagrange function L = Ekin - Epot. They lead to equations of motion of the form
- .
In the case of n torsion angles as degrees of freedom, the n × n mass matrix M(θ) and the n-dimensional vector , can be calculated explicitly (Mazur & Abagyan, 1989; Mazur et al., 1991). To generate a trajectory this linear set of n equations would have to be solved in each time step for the torsional accelerations , formally by
- .
This requires a computational effort proportional to n3, which is prohibitively expensive for larger systems. Therefore, in CYANA the fast recursive algorithm of (Jain et al., 1993) is implemented to compute the torsional accelerations, which makes explicit use of the tree structure of the molecule in order to obtain with a computational effort that is only proportional to n. The mathematical details and a proof of correctness of the CYANA torsion angle dynamics algorithm are given in (Jain et al., 1993).
Torsional accelerations
The algorithm of (Jain et al., 1993) computes a factorization of the inverse of the mass matrix, M(θ)-1, into a product of highly sparse matrices with non-zero elements only in 6 × 6 blocks on or near the diagonal. As a result, the torsional accelerations can be obtained by executing a series of three linear loops over all rigid bodies similar to the single loop that is needed to compute the kinetic energy, Ekin.
The computation of the torsional accelerations by the algorithm of Jain et al. (1993) is initialized by calculating for all rigid bodies, k = 1,…,n, the six-dimensional vectors ak, ek and zk:
- ,
- ,
- ,
and the 6 × 6 matrices Pk and φk:
- ,
- .
03 is the 3 × 3 zero matrix, 13 is the 3 × 3 unit matrix, and A(y) denotes the antisymmetric 3 × 3 matrix associated with the cross product, i.e., A(y)x = y Λ x for all vectors x.
Next, several auxiliary quantities are calculated by executing a recursive loop over all rigid bodies in the backward direction, k = n,n - 1,…,1:
Dk and εk are scalars, Gk is a six-dimensional vector, and “←” means: “assign the result of the expression on the right hand side to the variable on the left hand side.” Finally, the tor-sional accelerations are obtained by executing another recursive loop over all rigid bodies in the forward direction, k = 1,…,n:
The auxiliary quantities αk are six-dimensional vectors, with α0 being equal to the zero vector.
Time step
Leap-frog algorithm
The integration scheme for the equations of motion in torsion angle dynamics (Mathiowetz et al., 1994) is a variant of the “leap-frog” algorithm used in Cartesian space molecular dynamics (Allen & Tildesley, 1987). To obtain a trajectory, the equations of motion are numerically integrated by advancing the i = 1,…,n (generalized) coordinates qi and velocities that describe the system by a small but finite time step Δt:
The degrees of freedom, qi, are the Cartesian coordinates of the atoms in conventional molecular dynamics simulation, or the torsion angles in CYANA. The O(Δt3) terms indicate that the errors with respect to the exact solution incurred by the use of a finite time step Δt are proportional to Δt3.
Temperature control
The time step Δt must be small enough to sample adequately the fastest motions. Because the fastest motions in conventional molecular dynamics simulation are oscillations of bond lengths and bond angles, which are “frozen” in torsion angle space, longer time steps can be used for torsion angle dynamics than for molecular dynamics in Cartesian space.
In practical applications with proteins time steps of about 100, 30 and 7 fs at low (1 K), medium (400 K) and high (10000 K) temperatures, respectively, can be used in torsion angle dynamics calculations with CYANA (Güntert et al., 1997), whereas time steps in Cartesian space molecular dynamics simulation generally have to be in the range of 2 ns. The concomitant fast exploration of conformation space provides the basis for the efficient CYANA structure calculation protocol.
The temperature is controlled by weak coupling to an external bath (Berendsen et al., 1984). Using a similar approach, the length of the time step is adapted automatically based on the accuracy of energy conservation (Güntert et al., 1997).
Time step
A time step, t → t + Δt, that follows a preceding time step, t - Δt' → t, consists of the following parts:
(1) On the basis of the torsional positions, θ(t), Coordinate generation of all atoms (Güntert, 1993).
(2) Using the Cartesian coordinates, calculate the target function, i.e. the potential energy function Epot(t) = Epot(θ(t)), and its gradient ∇Epot(t).
(3) Determine the time-step, Δt = λεΔt', using the time-step scaling factor
- .
λε is based on the reference value for the relative accuracy of energy conservation, εref, and on the relative change of the total energy, E = Ekin + Epot, in the preceding time-step, ε(t), as given by
- .
is the maximally allowed value of the scaling factor, which is set to 1.025 in CYANA. The time constant, τ >> 1, is a user-defined parameter that is measured in units of the time-step. Typically, a value of τ = 20 is used for structure calculations with CYANA. To calculate ε(t), the total energy E(t) is evaluated before velocity scaling is applied (step 4 below), whereas for E(t - Δt') the value after velocity scaling in the preceding time-step is used. Thus, the measurement of the accuracy of energy conservation is not affected by the scaling of velocities. An exact algorithm would yield E(t) = E(t - Δt') and consequently ε(t) = 0.
(4) Adapt the temperature by scaling of the torsional velocities, i.e., replace by and by (see step 7 below for the definition of ). The velocity scaling factor, λT, is given by (Berendsen et al., 1984)
- ,
where Tref is the reference value of the temperature. The instantaneous temperature, T(t), is given by T(t) = 2 Ekin(t)/nkB, where Ekin(t) is the kinetic energy at time t, n denotes the number of torsion angles and kB is the Boltzmann constant. Temperature control by coupling to an external heat bath (and time-step control) can be turned off by setting τ = ∞.
(5) Calculate the torsional accelerations, , using equations [3–6].
(6) Calculate the new velocities at half time-step,
- .
(7) Calculate the new estimated velocities at full time step,
- .
(8) Calculate the new torsional positions,
- .
The algorithm is initialized by setting t = 0, Δt' = Δt and . The initial torsional velocities, , are chosen randomly from a normal distribution with zero mean value and a standard deviation which ensures that the initial temperature has a predefined value, T(0). Once the time step t → t + Δt is completed by going through the operations 1 to 8, t is replaced by t + Δt, and Δt' by Δt.
Accuracy of acceleration calculation
Unlike the situation in Cartesian dynamics, where the accelerations are a function of the positions only, the torsional accelerations also depend on the velocities. These, however, are only known at half time-steps, whereas the positions and accelerations are required at full time-steps. In step 7 the presently used algorithm employs linear extrapolation to obtain an estimate of the velocity after the full time-step, , which is used in the next integration step to calculate the torsional accelerations (step 5). They are therefore beset with an additional error that could be eliminated by iterating the steps 5–7. In general, no significant improvement can be observed after one iteration (Mathiowetz et al., 1994). Using instead of introduces an additional error of order O(Δt3) into the velocity calculation of the leap-frog algorithm in step 6. However, the intrinsic accuracy of the velocity step is also O(Δt3). Thus, using the estimated velocities, , does not change the order of accuracy of the integration algorithm. Each iteration of steps 5–7 requires the calculation of the torsional accelerations which, in general, takes as long as the calculation of the target function and its gradient. It is therefore more efficient to slightly decrease the time step, Δt, than to perform steps 5–7 twice in each integration step. The situation could be different if a full physical force field were used, since then the calculation of torsional accelerations would require only a negligible fraction of the total computation time.
Since in structure calculations with torsion angle dynamics the time-steps are made as long as possible a safeguard against occasional strong violations of energy conservation was introduced: If the total energy, E, has changed by more than 10% in a single time-step, this time-step is rejected and replaced by two time-steps of half length.
References
ABE, H., BRAUN, W., NOGUTI, T. & GO, N. (1984). Rapid calculation of 1st and 2nd derivatives of conformational energy with respect to dihedral angles for proteins - General recurrent equations. Computers & Chemistry 8, 239–247.
ALLEN, M. P. & TILDESLEY, D. J. (1987). Computer simulation of liquids. Oxford: Clarendon Press.
ARNOLD, V. I. (1978). Mathematical methods of classical mechanics. New York: Springer.
BERENDSEN, H. J. C., POSTMA, J. P. M., VAN GUNSTEREN, W. F., DINOLA, A. & HAAK, J. R. (1984). Molecular dynamics with coupling to an external bath. Journal of Chemical Physics 81, 3684-3690.
BRÜNGER, A. T. (1992). X-PLOR, Version 3.1. A System for X-ray Crystallography and NMR. New Haven, CT: Yale University Press.
GÜNTERT, P. (1993). Neue Rechenverfahren für die Proteinstrukturbestimmung mit Hilfe der magnetischen Kernspinresonanz. Ph.D. thesis, ETH.
GÜNTERT, P., BRAUN, W. & WÜTHRICH, K. (1991). Efficient computation of three-dimensional protein structures in solution from nuclear magnetic resonance data using the program DIANA and the supporting programs CALIBA, HABAS and GLOMSA. Journal of Molecular Biology 217, 517–530.
GÜNTERT, P., MUMENTHALER, C. & WÜTHRICH, K. (1997). Torsion angle dynamics for NMR structure calculation with the new program DYANA. Journal of Molecular Biology 273, 283–298.
GÜNTERT, P. & WÜTHRICH, K. (2001). Sampling of conformation space in torsion angle dynamics calculations. Computer Physics Communications 138, 155–169.
JAIN, A., VAIDEHI, N. & RODRIGUEZ, G. (1993). A fast recursive algorithm for molecular dynamics simulation. Journal of Computational Physics 106, 258–268.
KIRKPATRICK, S., GELATT, C. D. & VECCHI, M. P. (1983). Optimization by Simulated Annealing. Science 220, 671–680.
KNELLER, G. R. & HINSEN, K. (1994). Generalized Euler equations for linked rigid bodies. Physical Review E 50, 1559–1564.
MATHIOWETZ, A. M., JAIN, A., KARASAWA, N. & GODDARD, W. A., III. (1994). Protein simulations using techniques suitable for very large systems: the cell multipole method for nonbond interactions and the Newton-Euler inverse mass operator method for internal coordinate dynamics. Proteins: Structure, Function, and Bioinformatics 20, 227–247.
MAZUR, A. K. & ABAGYAN, R. A. (1989). New methodology for computer-aided modeling of biomolecular structure and dynamics 1. Non-cyclic structures. Journal of Biomolecular Structure & Dynamics 6, 815–832.
MAZUR, A. K., DOROFEEV, V. E. & ABAGYAN, R. A. (1991). Derivation and testing of explicit equations of motion for polymers described by internal coordinates. Journal of Computational Physics 92, 261–272.
NILGES, M., CLORE, G. M. & GRONENBORN, A. M. (1988). Determination of three-dimensional structures of proteins from interproton distance data by hybrid distance geometry-dynamical simulated annealing calculations. FEBS Letters 229, 317–324.
SCHULTZE, P. & FEIGON, J. (1997). Chirality errors in nucleic acid structures. Nature 387, 668-668.